最小二乘法权函数是回归分析中的一种重要概念,用于量化每个样本点对回归线的影响程度。在求解最小二乘法权函数时,通常需要先确定回归模型的参数,然后计算每个样本点的残差平方和,最后根据残差平方和计算权函数。权函数的求解涉及到矩阵运算和代数运算,需要一定的数学基础。在回归分析中,权函数的求解对于提高模型的准确性和稳定性具有重要意义。
本文目录导读:
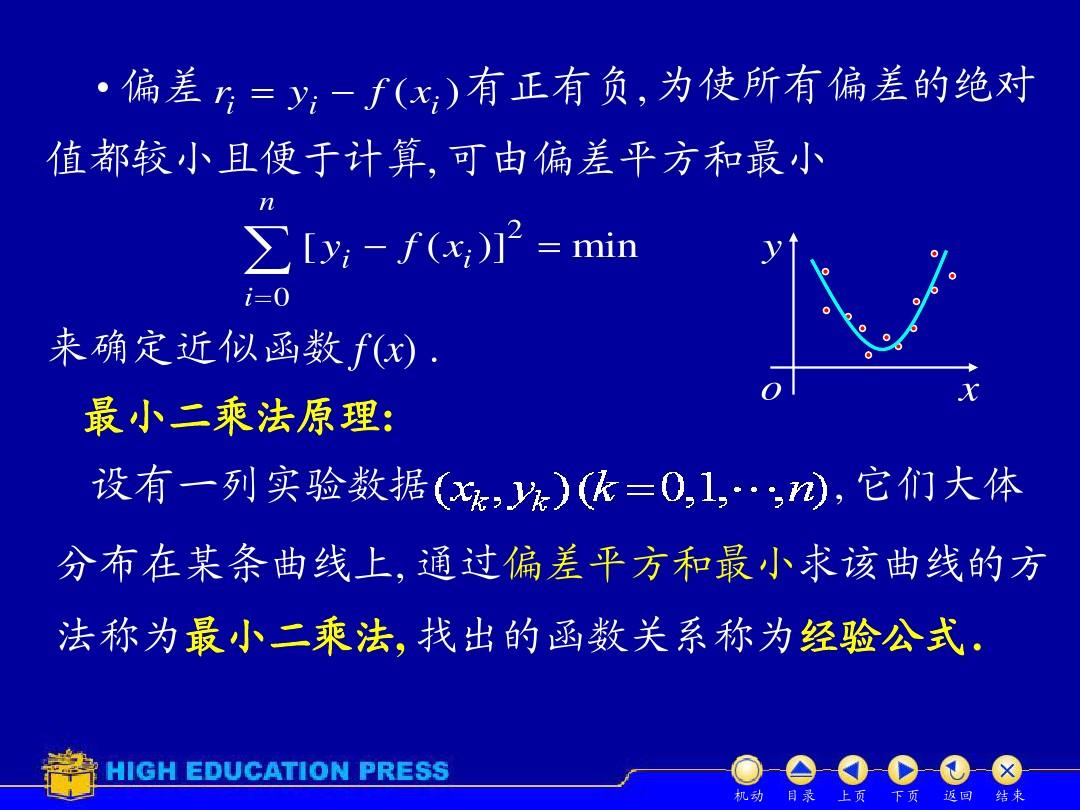
最小二乘法是一种数学优化技术,它通过最小化误差的平方和来寻找数据的最佳函数匹配,在统计学、生物信息学、金融和工程等领域,最小二乘法被广泛应用,本文旨在探讨在最小二乘法中如何求解权函数。
最小二乘法的原理
最小二乘法的基本原理是:对于给定的数据集,通过最小化误差的平方和来求解未知参数,这些未知参数可以是线性回归模型中的斜率和截距,也可以是非线性模型中的其他参数。
权函数的定义
在最小二乘法中,权函数是用于调整数据点权重的一个函数,它可以帮助我们处理数据中的噪声和异常值,从而提高模型的稳健性和准确性,权函数通常是一个正数函数,且对于不同的数据点,权函数的值可以不同。
求解权函数的方法
求解权函数是应用最小二乘法的一个关键步骤,我们可以采用以下步骤来求解权函数:
1、数据预处理:需要对数据进行预处理,包括去除噪声和异常值,以及进行数据标准化等,这些预处理步骤有助于提高模型的稳健性和准确性。
2、设定权函数形式:根据数据的特性和分析需求,设定合适的权函数形式,常见的权函数形式包括常数权函数、线性权函数和对数权函数等。
3、求解未知参数:通过最小化误差的平方和来求解未知参数,这些未知参数可以是权函数中的参数,也可以是其他模型参数。
4、验证模型:对求解得到的模型进行验证,包括绘制残差图、计算预测误差等,以确保模型的准确性和可靠性。
示例分析
为了更好地说明如何求解权函数,我们可以考虑一个简单的线性回归模型,假设我们有一组数据点 (x, y),x 是自变量,y 是因变量,我们想要通过最小二乘法来求解直线 y = ax + b 的斜率和截距 a 和 b,同时考虑权函数 w(x)。
1、数据预处理:假设我们已经去除了数据中的噪声和异常值,并进行了数据标准化处理。
2、设定权函数形式:我们设定权函数 w(x) 为一个线性函数,即 w(x) = mx + c,我们需要求解的参数包括 a、b、m 和 c。
3、求解未知参数:通过最小化误差的平方和来求解未知参数,具体地,我们需要最小化以下目标函数:
J(a, b, m, c) = ∑[y - (ax + b)(mx + c)]^2其中,∑表示对所有数据点进行求和。
4、验证模型:对求解得到的模型进行验证,包括绘制残差图、计算预测误差等,以确保模型的准确性和可靠性。
本文探讨了最小二乘法中权函数的求解方法,通过设定合适的权函数形式,并利用最小化误差的平方和来求解未知参数,我们可以得到更稳健和准确的模型,随着数据科学和机器学习的不断发展,最小二乘法将在更多领域得到应用,我们期待更多创新方法和技术能够推动这一领域的进步。



 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号